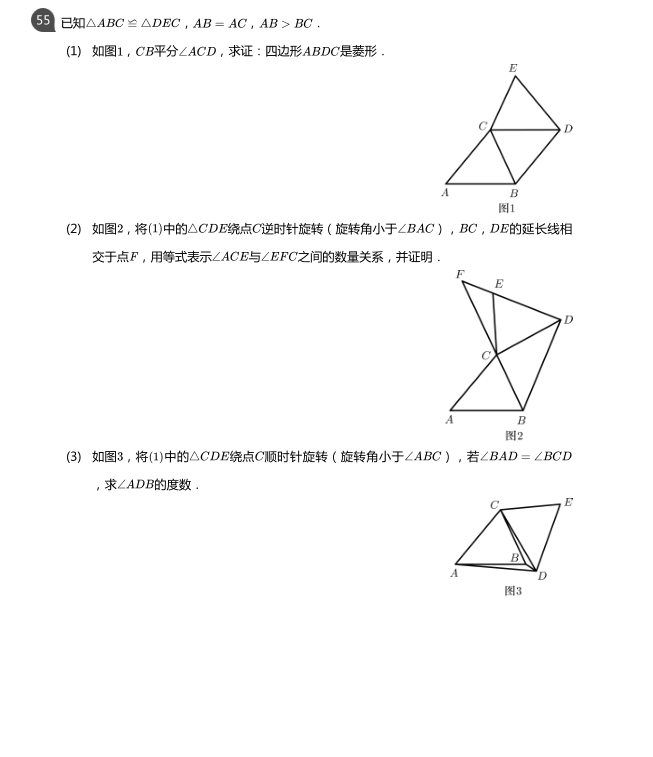
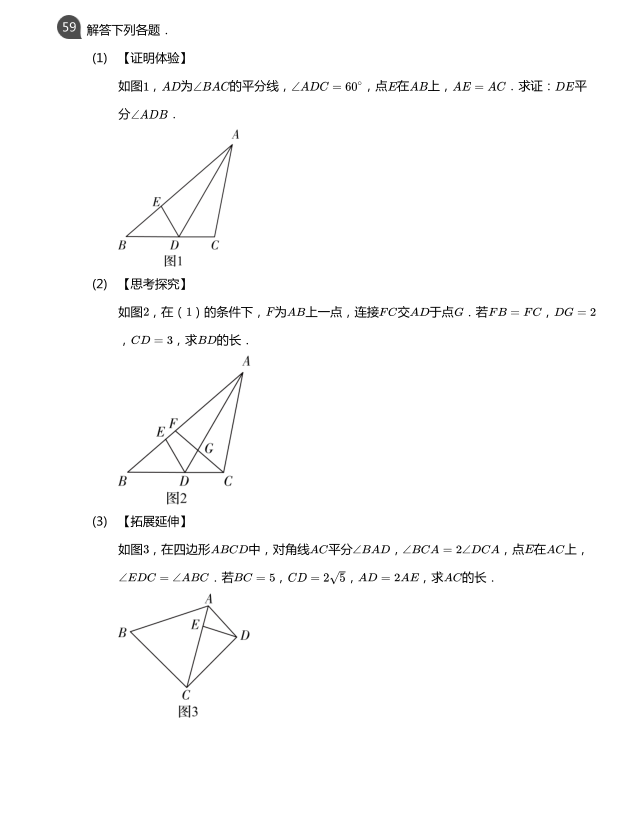
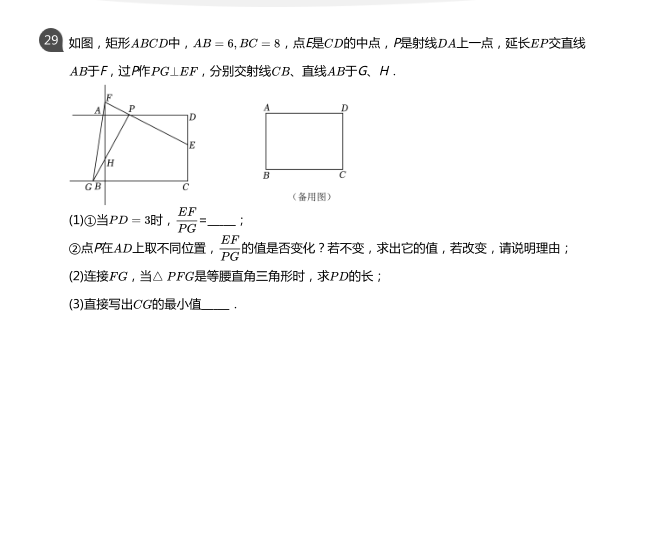
★重点★正、反比率函数,一次、二次函数的图象和性质。
☆内容提要☆
1、平面直角坐标系
1.各象限内点的坐标的特征
2.坐标轴上点的坐标的特征
3.关于坐标轴、原点对称的点的坐标的特征
4.坐标平面内点与有序实数对的对应关系
2、函数
1.表示办法:⑴分析法;⑵列表法;⑶图象法。
2.确定自变量取值范围的原则:⑴使代数式有意义;⑵使实质问题有
意义。
3.画函数图象:⑴列表;⑵描点;⑶连线。
3、几种特殊函数
(概念图象性质)
1.正比率函数
⑴概念:y=kx(k=?0)或y/x=k。
⑵图象:直线(过原点)
⑶性质:①k0,②k0,
2.一次函数
⑴概念:y=kx+b(k=?0)
⑵图象:直线过点(0,b)与y轴的交点和(-b/k,0)与x轴的交点。
⑶性质:①k0,②k0,
⑷图象的四种状况:
3.二次函数
⑴概念:
特殊地,都是二次函数。
⑵图象:抛物线(用描点法画出:先确定顶点、对称轴、开口方向,再对称地描点)。用配办法变为,则顶点为(h,k);对称轴为直线x=h;a0时,开口向上;a0时,开口向下。
⑶性质:a0时,在对称轴左边,右边;a0时,在对称轴左边,右边。
4.反比率函数
⑴概念:或xy=k(k=?0)。
⑵图象:双曲线(两支)用描点法画出。
⑶性质:①k0时,图象坐落于,y随x;②k0时,图象坐落于,y随x;③两支曲线无限接近于坐标轴但永远不可以到达坐标轴。
4、要紧解题办法
1.用待定系数法求分析式(列方程[组]求解)。对求二次函数的分析式,要合理使用一般式或顶点式,并应充分运用抛物线关于对称轴对称的特征,探寻新的点的坐标。
2.借助图象一次(正比率)函数、反比率函数、二次函数中的k、b;a、b、c的符号。